GEODIFF: 基于扩散模型的分子构象生成
Published:
Paper Address: GEODIFF: A GEOMETRIC DIFFUSION MODEL FOR MOLECULAR CONFORMATION GENERATION
概要
药物设计是一个漫长且代价高昂的过程,随着深度学习技术的出现,利用高效的深度学习技术介入药物设计成为了目前的研究热点。在药物设计中一个重要的领域是分子从头生成(De novo Molecular Design),旨在生成所需特性的分子。由于分子化学空间巨大,传统方法效率低下,深度生成模型例如VAE, GAN, RNN, Flow等在生成图片,文本以及音频等表现良好,所以考虑利用生成模型设计新的分子。最近,发现了生成模型的一种新的范式——扩散模型(Diffusion Models),将马尔可夫链和神经网络结合,利用VAE和Flow模型的思想,获得了不错的效果。对于分子生成领域,通常将分子表示为一维的SMILES, 二维的Graph和三维的Conformation,3D conformation具有较为丰富的空间信息,大大改善生成效果。因此,本文作者提出GEODIFF模型,该模型结合扩散模型和3D构象信息,在保证将分子构象的旋转平移不变性建模的同时,在3D构象生成上性能达到同时期的SOTA。
1 论文和代码地址

论文题目:GEODIFF: A GEOMETRIC DIFFUSION MODEL FOR MOLECULAR CONFORMATION GENERATION
发表单位:未知
论文地址:https://openreview.net/forum?id=JRrjhY3sJy(ICLR 2022 openReview)
代码地址:无
提交时间:2021年9月29日
2 动机
由于分子的3D构象比一维的字符串SMILES,二维的分子图Graph更具有内在的和更丰富的信息,并且分子的3D结构确定了其生物学和物理性质,但3D构象生成过程不稳定且较为复杂,过去的3D构象生成模型可分为三类,第一类是传统方法,利用分子动力学或者马尔科夫链蒙特卡洛算法(MCMC),第二类是基于中间变量的深度生成模型,第三类则是基于梯度场的深度生成模型。这三类模型存在以下问题:
传统方法:采样耗费时间,当分子量和原子数增大时,效率低下。
基于中间变量的:在利用graph生成分子构象时,实际上存在较大的冗余,因为分子本身存在6个自由度的冗余,在旋转和平移时,虽然分子本身不会改变,但是却改变了分子的坐标,因此在生成构象时需要考虑分子构象的旋转平移不变性。虽然分子坐标不具有旋转平移不变性,但是分子间的距离有着天然的这种性质,因此很多模型先通过预测距离再生成构象[1],在这一过程中产生了积累误差,预测距离的模型本身存在误差加上构象生成的误差,会产生一个Two-stage的误差。
基于梯度场的:针对上述积累误差问题,研究者选择学习似然函数的梯度场(可看成作用于原子上的伪合力),利用Score-based的生成模型生成分子构象[2],然而作者认为通过 Score-based Model学习距离梯度,该模型在实作中被输入距离矩阵,其可能违反triangular inequality原则或甚至包含负值。结果,该模型实际上在训练时学习的时不合法的距离矩阵,测试时输入是正常的构象,两者分布极为不同。
针对上述问题,作者提出了GEODIFF,直接在原子上作改变,并保证旋转平移不变性,有效的生成分子的3D构象。
3 方法
该解决方案是基于去噪扩散模型,受到热力学的扩散过程的启发,将原子视为热力学系统中的粒子,不断通过向数据中添加高斯噪声,破坏数据结构(扩散过程)直到拟合标准的高斯分布,再逐渐恢复数据结构(逆向生成过程),其中,扩散过程为一个固定参数的马尔科夫链,逆向过程为一个带有参数的神经网络。扩散模型的具体思想和详细推导可参见[3, 4],这里不再赘述。
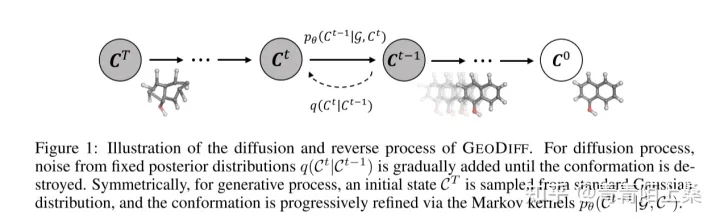
上图为模型的基本过程,其中
正向过程的公式如下, \(\mathcal{C}^{0}\)为原始构象数据,随着时间步\(t\)的增加,逐渐添加高斯噪声,\(T\)时间步为已知的标准高斯分布(先验):
\[q\left(\mathcal{C}^{1: T} \mid \mathcal{C}^{0}\right)=\prod_{t=1}^{T} q\left(\mathcal{C}^{t} \mid \mathcal{C}^{t-1}\right), \quad q\left(\mathcal{C}^{t} \mid \mathcal{C}^{t-1}\right)=\mathcal{N}\left(\mathcal{C}^{t} ; \sqrt{1-\beta_{t}} \mathcal{C}^{t-1}, \beta_{t} I\right)\]逆向过程如下,在逆向过程中加入分子的Graph,同样经过\(T\)个时间步:
\[p_{\theta}\left(\mathcal{C}^{0: T-1} \mid \mathcal{G}, \mathcal{C}^{T}\right)=\prod_{t=1}^{T} p_{\theta}\left(\mathcal{C}^{t-1} \mid \mathcal{G}, \mathcal{C}^{t}\right), \quad p_{\theta}\left(\mathcal{C}^{t-1} \mid \mathcal{G}, \mathcal{C}^{t}\right)=\mathcal{N}\left(\mathcal{C}^{t-1} ; \mu_{\theta}\left(\mathcal{G}, \mathcal{C}^{t}, t\right), \sigma_{t}^{2} I\right)\]逆向过程要遵循一个重要性质就是旋转平移不变性,因此作者的想法是:
令\(p\left(x_{T}\right)\)具有旋转不变性,如\(p\left(x_{T}\right)\)果具有,则\(p\left(x_{T}\right)=p\left(T_{g}\left(x_{T}\right)\right)\)成立, 同时,如果\(p\left(x_{t-1} \mid x_{t}\right)\)也具有,则\(p_{\theta}\left(x_{0}\right)=\int p\left(x_{T}\right) p_{\theta}\left(x_{0: T-1} \mid x_{T}\right) \mathrm{d} \boldsymbol{x}_{1: T}\)就会具有。 目标即为\(p\left(x_{T}\right)\)和\(p\left(x_{t-1} \mid x_{t}\right)\)需要具有旋转平移不变性(Equivariance)。
群:一种集合加上一种运算的代数结构 Equivariance可以参考抽象代数中群中的映射。 在抽象代数中,即为一个群(group)的映射,变换输入,并将其映射到某个输出,和先映射再变换,输出结果相同。 SE(3)群是一类特殊的群,由刚性变换组成,刚体可以在空间中连续运动。 所以Equivariance应该是一个在刚性运动下等变的分布,即去除质心(zero-CoM)的各向同性高斯分布。
作者引入zero-CoM(CoM:质心)思想[去除质心],可同时具有旋转和平移不变性。 和VAE类似,由于数据分布概率的难以求解,近似求解其变分下届,最终目标函数为:(具体可推导参考[3])
\[\begin{aligned} \mathbb{E}\left[\log p_{\theta}\left(\mathcal{C}^{0} \mid \mathcal{G}\right)\right] &=\mathbb{E}\left[\log \mathbb{E}_{q\left(\mathcal{C}^{1: T} \mid \mathcal{C}^{0}\right)} \frac{p_{\theta}\left(\mathcal{C}^{0}: T\right.}{q\left(\mathcal{C}^{1: T} T \mid \mathcal{C}^{0}\right)}\right] \\ & \geq-\mathbb{E}_{q}\left[\sum_{t=1}^{T} D_{\mathrm{KL}}\left(q\left(\mathcal{C}^{t-1} \mid \mathcal{C}^{t}, \mathcal{C}^{0}\right) \| p_{\theta}\left(\mathcal{C}^{t-1} \mid \mathcal{C}^{t}, \mathcal{G}\right)\right)\right]:=-\mathcal{L}_{\mathrm{ELBO}} \end{aligned}\]采样过程如下:

4 实验结果
在分子数据集GEOM-QM9和GEOM-Drugs上实验,GeoDiff始终优于最先进的ML模型,尤其是对于更具挑战性大分子(药物数据集),并且展示了GeoDiff模拟多模态分布的优越能力,以及生成准确和多样化的构象。
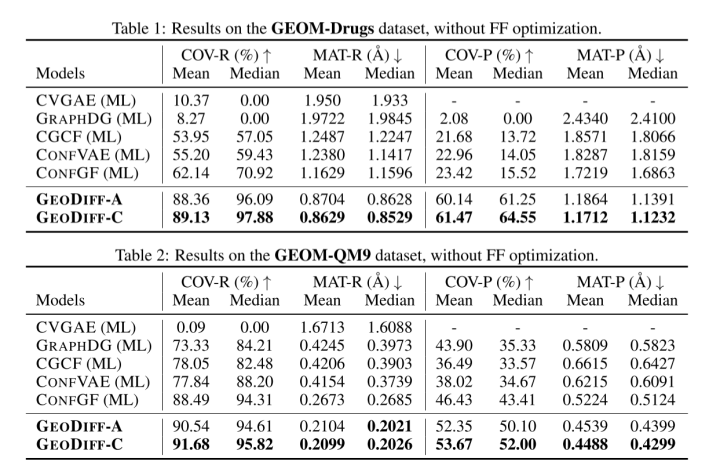
5 总结
作者提出了一种用于产生分子构象的新概率模型Geodiff。多个任务的综合实验表明,GeoDiff与现有最先进的模型相比具有较大竞争力。未来的工作将包括进一步改进或加速模型的扩散模型的其他进展,并将方法延伸到生成蛋白质等更具挑战性的任务。
Reference
[1] Minkai Xu, Shitong Luo, Yoshua Bengio, Jian Peng, and Jian Tang. Learning neural generative dynamics for molecular conformation generation. In International Conference on Learning Representations, 2021a. https://arxiv.org/abs/2102.10240
[2] Chence Shi, Shitong Luo, Minkai Xu, and Jian Tang. Learning gradient fields for molecular conformation generation. In International Conference on Learning Representations, 2021. https://arxiv.org/abs/2105.03902
[3] https://lilianweng.github.io/lil-log/2021/07/11/diffusion-models.html
[4] https://www.techbeat.net/talk-info?id=524
